METODO DE CRAMER CON TRES INCOGNITAS

METODO DE CRAMER

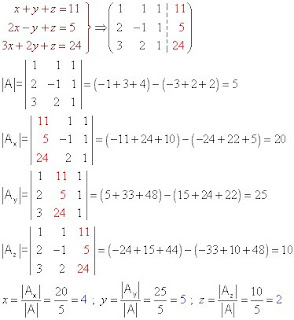La regla de Cramer es un teorema en álgebra lineal, que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor a Gabriel Cramer (1704 - 1752).
Si es un sistema de ecuaciones. A es la matriz de coeficientes del sistema, es el vector columna de las incógnitas y es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b.

Es aplicable si el sistema tiene igual número de ecuaciones que de incógnitas n=m y el determinante de la matriz de coeficientes es distinto de cero. Es decir, un sistema de Cramer es, por definición, compatible determinado y, por tanto, tiene siempre una solución única.
El valor de cada incógnita xi se obtiene de un cociente cuyo denominador es el determinante de la matriz de coeficientes, y cuyo numerador es el determinante que se obtiene al cambiar la columna i del determinante anterior por la columna de los términos independientes.